Contents
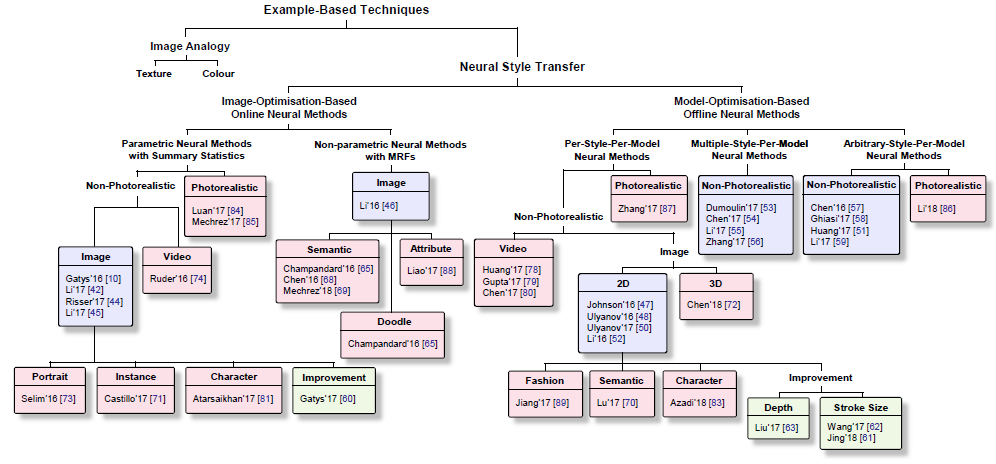
- Image-Optimisation-Based Online Neural Methods
- Parametric Neural Methods with Summary Statistics
- Gatys et al, “A Neural Algorithm of Artistic Style”, 2015.
- Li et al, “Demystifying Neural Style Transfer”, 2017.
- Li et al. “Laplacian-Steered Neural Style Transfer”, 2017.
- Non-parametric Neural Methods with MRFs
- Parametric Neural Methods with Summary Statistics
위 그림에서 볼 수 있듯, NST 알고리즘들은 크게 IOB-IR, MOB-IR로 나눌 수 있다. 이번 글에서는 그 중 IOB-IR 알고리즘들을 대표적인 논문들을 통해 알아본다.
Image-Optimisation-Based Online Neural Methods
Parametric Neural Methods with Summary Statistics
Parametric IOB-IR 알고리즘의 핵심은 생성할 이미지의 Style Information은 Style Image에 맞추고, Content Image는 Content Image에 맞추는 것이다. 그에 따라 각각의 “Information”을 어떻게 추출할지에 대해 주로 연구가 되어왔다.
Gatys et al, “A Neural Algorithm of Artistic Style”, 2015.
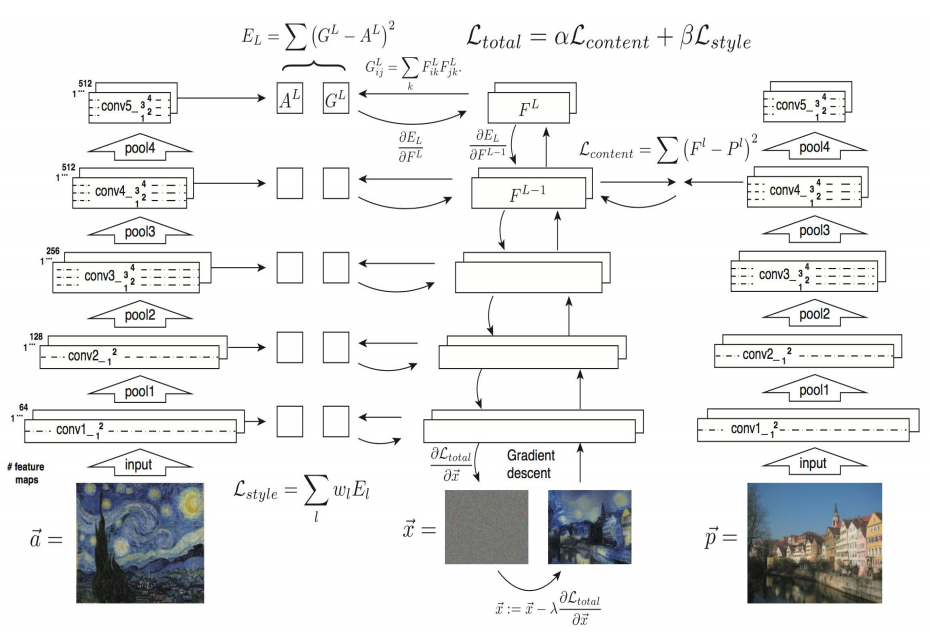
NST의 효시격 논문인 이 논문에서는 \(I_{output}\), \(I_{content}\), \(I_{style}\) 세 이미지에 대해 다음과 같은 Loss Function을 정의한 뒤, 이 Loss를 최소화시키는 방향으로 \(I_{output}\) 를 optimize한다.
\[L_{total} = \alpha L_{content} + \beta L_{style} \]
\(L_{content}\) 와 \(L_{style}\) 은 다음과 같이 정의된다.
- \(F_l\): \(I_{output}\) 를 VGG Network의 통과시켰을 때, \(l\)번째 레이어의 feature map
- \(P_l\): \(I_{content}\) 를 VGG Network의 통과시켰을 때, \(l\)번째 레이어의 feature map
- \(S_l\): \(I_{style}\) 를 VGG Network의 통과시켰을 때, \(l\)번째 레이어의 feature map
\(Gram(X)\) 는 주어진 행렬 X에 대한 Gram matrix를 의미하며, feature map의 경우 \(C \times W \times H\) 3-dim array이기 때문에 \(C(=N_l) \times HW(=M_l)\) 로 reshape하여 Gram matrix를 계산한다. 이때, 행렬 X에 대한 Gram matrix는 다음과 같다.
더 쉽게 표현하면, \(Gram(X) = X \cdot X^T\) 이다.
이 논문에서는 \(l\), 즉 각 Loss를 계산할 때 어떤 layer를 선택했는지가 중요한 요소라고 한다. 기본적으로 \(L_{content}\) 를 계산할때는 \(conv4_2\), \(L_{style}\) 에서는 \({conv1_1, conv2_1, conv3_1, conv4_1, conv5_1}\) 을 사용했으며(relu까지 포함), 네트워크는 pretrained VGG19를 사용하며, 이 네트워크는 업데이트되지 않고 오직 \(I_{output}\) 만 업데이트된다.
\(\alpha\) 와 \(\beta\) 의 비율을 어떻게 하느냐에 따라 \(I_{output}\) 이 \(I_{content}\) 에 가까운지, \(I_{style}\) 에 가까운지가 결정되는데, \(\alpha / \beta\) 비율을 크게할 수록 이미지의 윤곽이 살고 작아질수록 스타일이 강해지는 것을 볼 수 있다.
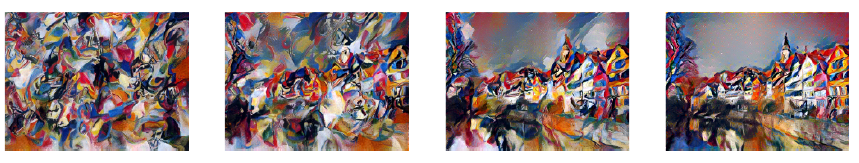
그 외 특이 사항으로는, VGG19 Network은 원래 Max pooling을 사용하나 Average pooling으로 이를 대체하였을 때 더 좋은 이미지 결과가 나왔다고 한다.
Contributions
- Ground truth 없이 style transfer를 수행
- Style image에 특별한 제한을 두지 않고도 수행이 가능
Limits
- Content image의 fine structure와 detail을 표현하지 못함
- CNN의 feature extractor가 low-level feature를 잃어버리기 때문
- Photo-realistic한 style transfer는 불가능
- 다양한 형태의 획과 칠을 표현하지 못하고, content image의 depth information을 잃어버림 (depth information이 무엇인지는 더 찾아 보아야 할 듯)
- Gram matrix가 왜 Style representation을 나타내는지 자세히 밝히지 못함
Gatys의 알고리즘은 Baseline으로 주로 사용되기 때문에 다소 길게 요약하였다.
Li et al, “Demystifying Neural Style Transfer”, 2017.
\(I_{output}\) 과 \(I_{style}\) 의 feature map에 Gram matrix를 씌운 값의 차이를 최소화 시키는게 왜 두 이미지의 Style을 비슷하게 만들까? 이에 대해 수학적으로 분석하고, 더 나아가 Gram matrix 외에도 다른 방법론을 제안한 논문이 Li의 논문 Demystifying Neural Style Transfer 이다. Gram matrix의 역할이 \(I_{output}\) 과 \(I_{style}\) 의 feature map의 distribution을 비슷하게 만드는 것임을 수학적으로 증명했다.
자세히 말하자면 MMD(Maximum Mean Discrepancy)를 최소화 시킴을 증명했는데, MMD는 두 분포 사이의 차이를 나타내는 측도로 KL-Divergence 등과 비슷한 맥락에 속한다. 이를 아주 간단히 설명하면 다음과 같다. 어떤 두 분포 \(p\) 와 \(q\) 가 있을 때, 이 둘이 서로 같을 필요 충분 조건은 임의의 함수 \(f\)에 대해 f(sample)의 기댓값이 같아야 한다는 것이다. 따라서, 이 두 기댓값의 차이를 MMD로 정의하며, 이를 두 분포 \(p\) 와 \(q\) 의 차이로 정의한다.(엄밀한 정리는 아래 사진에 있으며, 도움이 될 자료도 첨부한다.)
여하튼 MMD를 정의하기 위해서는 함수 \(f\)(=커널 $k$)가 정의되어야하는데, Gram matrix는 이 kernel이 qudratic polynomial인 경우이며, 따라서 Gram matrix를 사용하는 것은 \(I_{output}\) 과 \(I_{style}\) 간의 MMD를 줄이는 효과를 가져왔다는 것이다.
MMD만 같게 하면 Style을 비슷하게 할 수 있다는 것에 착안해 다른 kernel(linear, gaussian, BN)들을 사용해 이들 경우에도 Style transfer가 잘 구현됨을 보였다. 이를 통해, DL에서 중요한 영역인 interpretation을 NST에 대해서도 설명할 수 있게 되었다는 의미가 있다.
Contributions
- Gatys의 알고리즘이 어떤 원리로 작동하는지 수학적으로 증명
- Image feature의 distribution 차이를 줄이는 것이 stylization의 한 방법임을 제시
Limits
- Gatys의 알고리즘이 가지고 있는 문제점들을 해결하지는 못함

Li et al. “Laplacian-Steered Neural Style Transfer”, 2017.
Gatys의 알고리즘은 Content Image의 형태를 왜곡하는 현상이 있었다. 이를 보완하기 위해 Li는 \(L_{style}\), \(L_{content}\) 에 이어 Laplacian Loss $L_{laplacian}$ 을 추가했다.
원본 이미지(좌)를 Laplacian filter에 통과 시키면 오른쪽 그림처럼 Edge 부분만 남게 되는데, \(I_{output}\) 과 \(I_{content}\) 의 Laplacian filter 통과 값의 차이를 추가 Loss Term으로 추가했으며, 식으로 표현하면 다음과 같다($D$는 Laplacian Operator).
이를 통해 Content Image의 형태를 잘 보존할 수 있게 되었다고한다.
Non-parametric Neural Methods with MRFs
Li et al. “Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis”, 2016.
NST 관련 논문 저자에 이 “Li”라는 이름이 자주 등장해서 NST 분야의 권위자인가 싶었는데, 알고보니 성씨만 같고 다 다른 사람이었다…
이 논문에서 Style Transfer를 적용하는 방법은 다음과 같다.
- \(I_{style}\) 과 \(I_{output}\) 을 pretrained VGG19 Network에 통과시킨다.
- 생성된 각각의 feature map \(F_s\), \(F_o\)를 \(k * k * C\) patch로 자른다.
- 각각의 patch set에 속해있는 patch를 서로 일대일 대응 시키는데, 이 때 patch 쌍의 Normalized cross correlation이 가장 작도록한다(이 과정에서도 Network가 쓰인다).
- 쌍을 이룬 style feature patch들의 L2 loss와 \(L_{content}\) 가 최소가 되도록 Image를 optimize한다.
여기서 3번에서의 Patch를 서로 대응 시키는 과정을 Patch Matching이라고 하는데, 이 논문에서는 Patch Matching 과정에 MRF prior를 도입하여 성능을 개선시켰다고 한다. 하지만 MRF에 대해 아직 공부를 하지 못해서 자세히는 모르겠다.
Patch matching은 \(I_{style}\), \(I_{content}\) 의 비슷한 부분을 매칭하여 stylize를 하는 효과를 가져오기 때문에, Content Image와 Style Image가 비슷한 모양을 가지고 있으면 뛰어난 성능을 보여주며, 특히 photorealistic한 경우에 image distortion이 적게 나타나 현실감있는 이미지를 생성한다. 하지만 같은 이유로 Content Image와 Style Image의 모양이 크게 다르면 잘 작동하지 않는다(위 사진의 두번째 행 참고).
참고로, 이 논문에서 Patch matching을 어떻게 구현했는지 아무리 찾아보려고 해도 논문 상에는 additional conv layer를 사용했다는 말 외에는 별 다른 설명이 없었다. Neural Matching이 원래부터 있던 알고리즘이기 때문에 생략한 것 같기도 한데… MRF NST 알고리즘을 공부하기 위해서는 MRF나 Neural Matching 등 사전 지식에 대한 공부가 많이 필요할 것 같다.
Summary
NST를 IOB-IR과 MOB-IR로 나누어 볼 때, 비교적 먼저 등장한 개념인 IOB-IR에 대표적인 논문 몇 가지를 살펴 보았다. Gatys의 알고리즘을 Baseline으로 이를 개선하려는 여러 시도들이 있었고, 주로 Loss term을 새로 추가, 수정 하는 방식으로 연구가 되어왔다.
다음 리뷰에서는 IOB-IR의 가장 큰 단점인 Inference Time을 개선할 수 있는 MOB-IR 카테고리에 대해 논문 리뷰와 함께 공부해 볼 예정이다.